The Phillips Curve & Aggregate Supply
Week 07
October 27, 2025
1. The Phillips Curve
The Pains of Fighting Inflation
. . .
“We have got to get inflation behind us. I wish there were a painless way to do that.” There isn’t .” Jerome Powel, Fed’s Chair, 21 Sept. 2022
. . .
The Phillips Curve (PC)
- Almarin Phillips discovered in the 1950s the kind of pain we have to suffer from reducing inflation.
- The PC shows how much more unemployment we will get \((\uparrow U)\), to reduce the inflation rate \((\downarrow \pi)\).
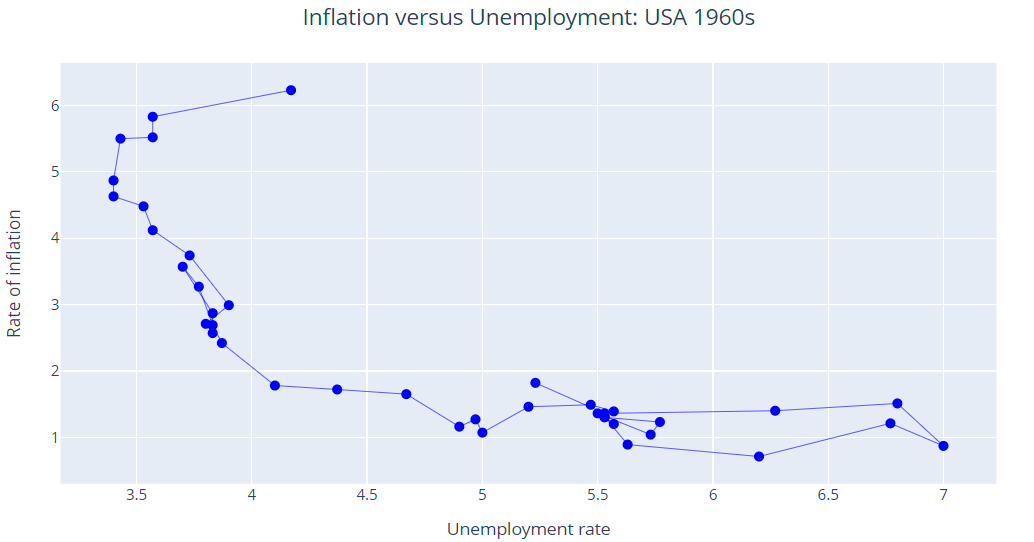
- The PC was easily confirmed in the 1960s.
- See next figure (click on any key)
 .
.
The Phillips Curve (PC)
In the 1960s, the PC was easy to spot and confirmed Phillips discovery.

The Phillips Curve in the 1970s
. . .
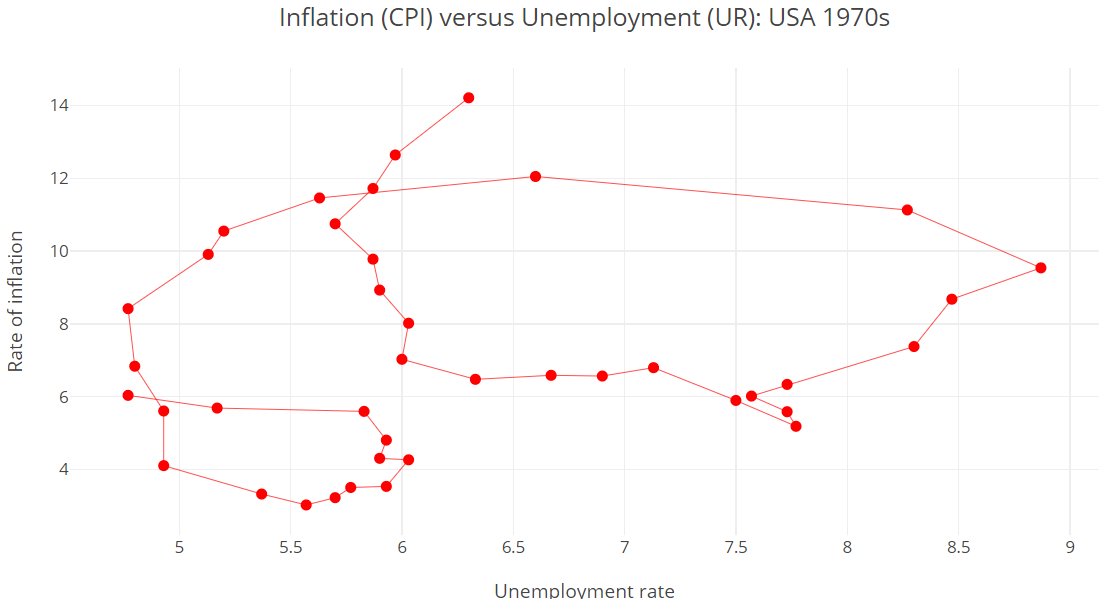
- In the 1970s, the PC begins to display a strange configuration: it seems to move constantly, looping around.
. . .
\(~~~~~\)
The Phillips Curve in the 1980s
. . .
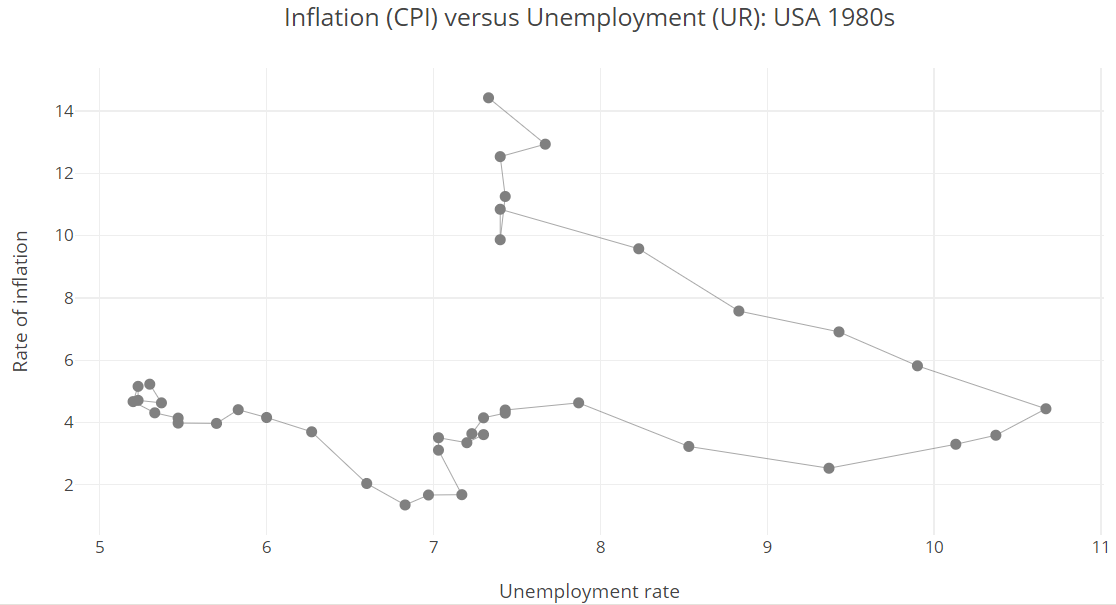
- In the 1980s, the PC seems to have different slopes.
. . .
\(~~~~~\)
The Friedman-Phelps PC Curve
Two Nobel prize winners – Milton Friedman and Edmund Phelps – showed how to write a PC that was able to explain those strange configurations.
Following them, the expectations-augmented Phillips Curve should be written as:
\[ \pi=\pi^e-\omega\left(U-U^n\right) \tag{7.1} \]
- \(\pi\) inflation rate
- \(U\) unemployment rate
- \(\omega\) is a parameter
- \(\pi^e\) expected inflation rate
- \(\left(U-U^n\right)\) cyclical unemployment rate
- \(U^n\) natural unemployment rate
Oil Price Shocks
. . .
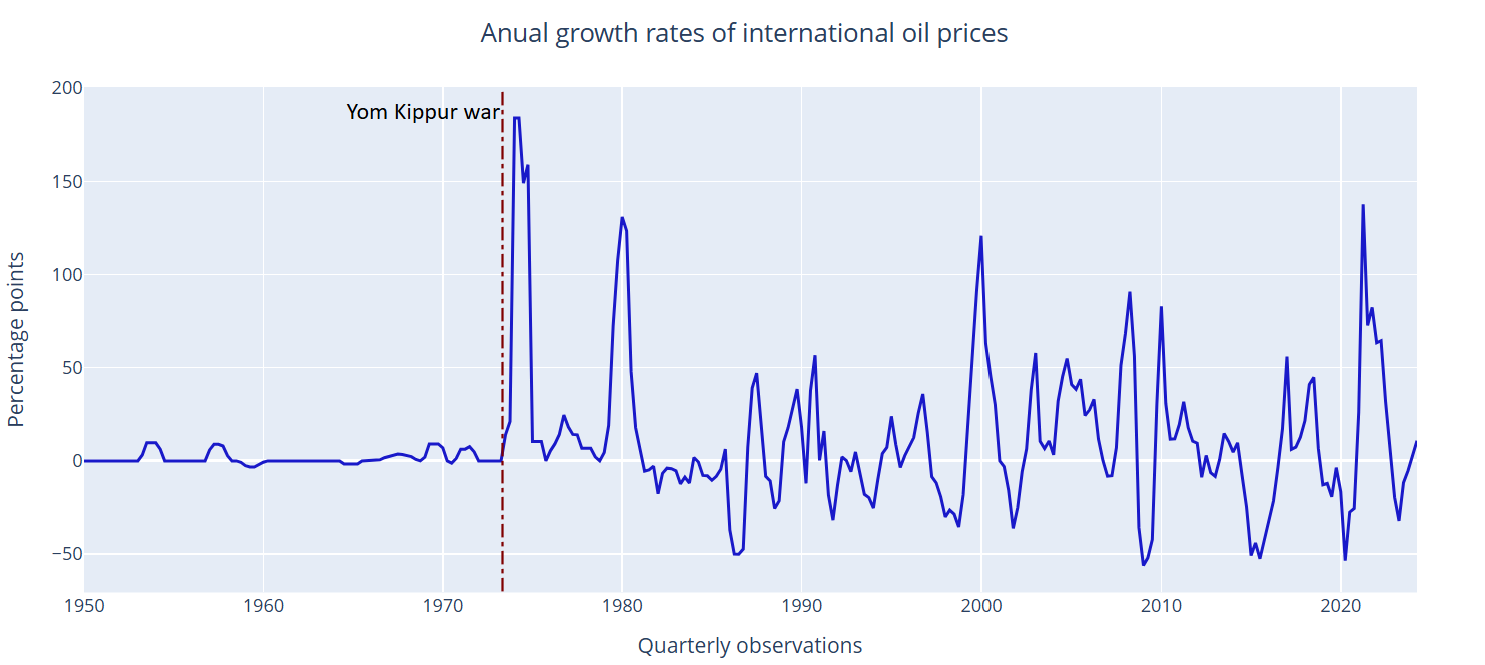
Large shocks in oil prices have been a recurrent major characteristic of the world economy since the early 1970s. They are temporary shocks.
. . .
The PC with Supply Shocks
- Shocks in oil prices affect production costs and as such they interfere in the relationship between inflation and unemployment.
- If oil prices increase a lot, production costs will also rise substantially, and inflation goes up, for every level of unemployment.
- The Covid19 pandemic has been a colossal shock on the supply side.
- The textbook calls these kind of shocks as temporary shocks: \[\color{red}{\rho}\]
- The PC can easily accommodate these temporary shocks:
\[ \pi=\pi^e-\omega\left(U-U^n\right)\class{fragment}{+ \color{red}{\rho}} \tag{7.2} \]
Inflation Expectations in the PC
- If inflation has been increasing recently, private agents expect that such trend will continue in the near future. A mathematical way of describing such a process is: \[\pi^e_t= \pi_{t-1} + \sigma(\pi_{t-1} - \pi_{t-2}) \tag{7.3}\]
- \(\pi^e_{t}\) is the inflation expectation for period \(t\).
- \(\pi_t\) and \(\pi_{t-1}\) are the inflation levels at periods \(t\) and \(t-1\).
- \(\sigma\) is a parameter of the degree of persistence of inflation expectations.
- To simplify the exposition, the textbook assumes that \(\sigma=0\), and we get: \[\pi^e_t= \pi_{t-1} \tag{7.4}\]
The PC with all Ingredients
The PC we will work with in this course includes three major ingredients:
- Trending (or adaptive) expectations: \(\quad \color{red}{\pi^e=\pi_{-1}}\)
- Cyclical unemployment: \(\quad \color{red}{\omega(U-U^n)}\)
- Temporary supply shocks: \(\quad \color{red}{\rho}\)
Therefore, the final version of the PC is given by:
\[ \pi=\pi_{-1}-\omega\left(U-U^n\right)+\rho \]
The PC: Graphical Representation
\[\pi=\pi^e-\omega\left(U-U^n\right)+\rho \quad , \quad \color{black}{\pi^e=\pi_{-1}}\]
- If we want a lower unemployment rate \((\downarrow U)\)
- We have to accept a higher inflation rate \((\uparrow \pi)\)
- Assuming everything else constant \(\left(U^n, \pi^e, \rho\right)\).
- Graphically, this can be represented as in the next figure (click on any key)
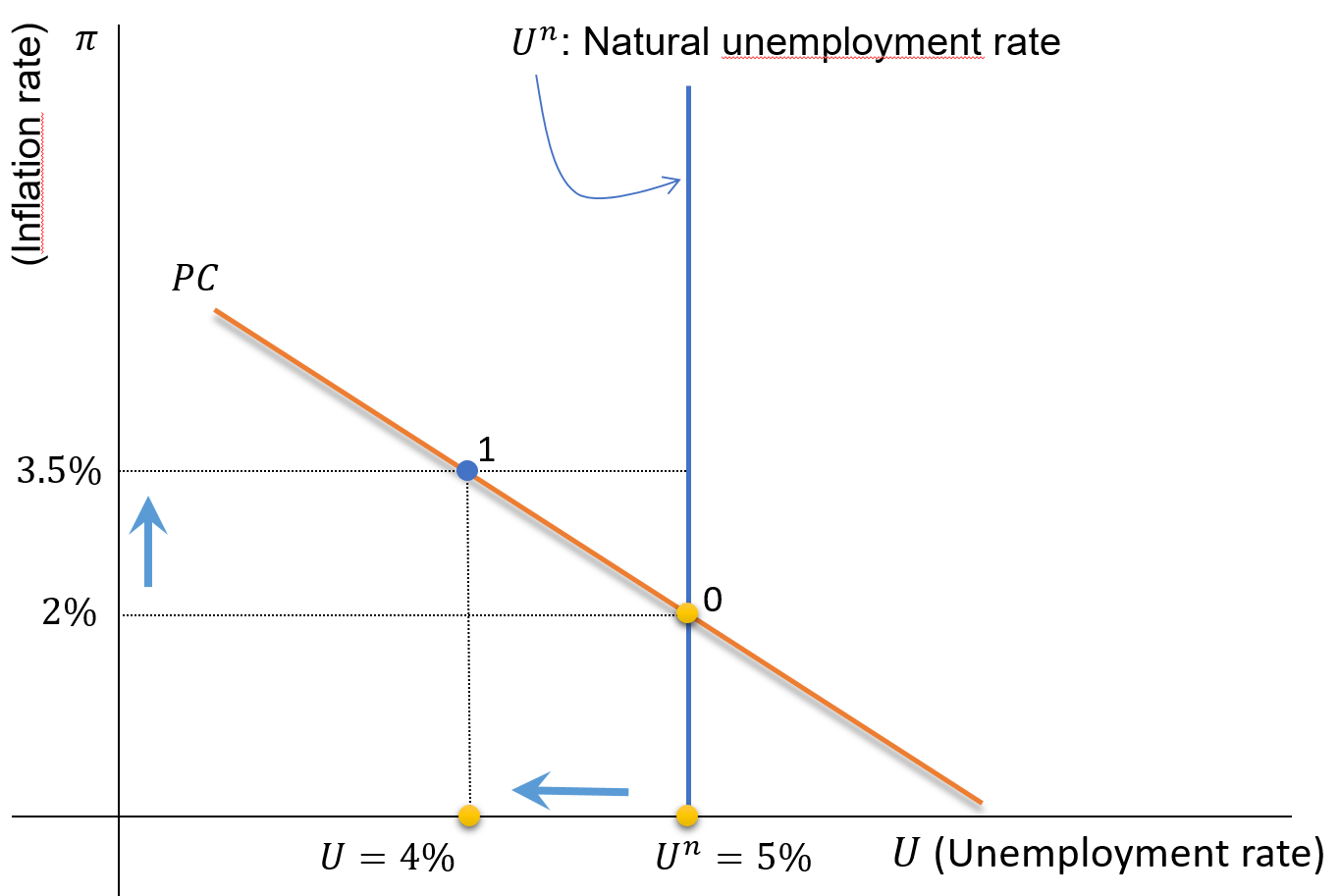
The PC: Graphical Representation
\[\pi=\pi^e-\omega\left(U-U^n\right)+\rho \quad , \quad \color{black}{\pi^e=\pi_{-1}}\]

Example:
- \(\pi_{-1} = 2\%\),
- \(\omega=1.5\)
- \(U^n=5\%\)
- If \(U=4\%\)
- \(U<U^n \Rightarrow \uparrow \pi\)
- \(\pi=3.5\%\)
2. Shifts in the Phillips Curve
Shifts in the Phillips Curve \((\pi^e , \ \rho)\)
\[\pi=\pi^e-\omega\left(U-U^n\right)+\rho \quad , \quad \color{black}{\pi^e=\pi_{-1}}\]
- The Phillips Curve shifts when the following forces change:
- Expected inflation (\(\pi^e\))
- Supply shocks (\(\rho\))
- Natural unemployment rate (\(U^n\))
- Let us concentrate on the first two forces (click on any key).
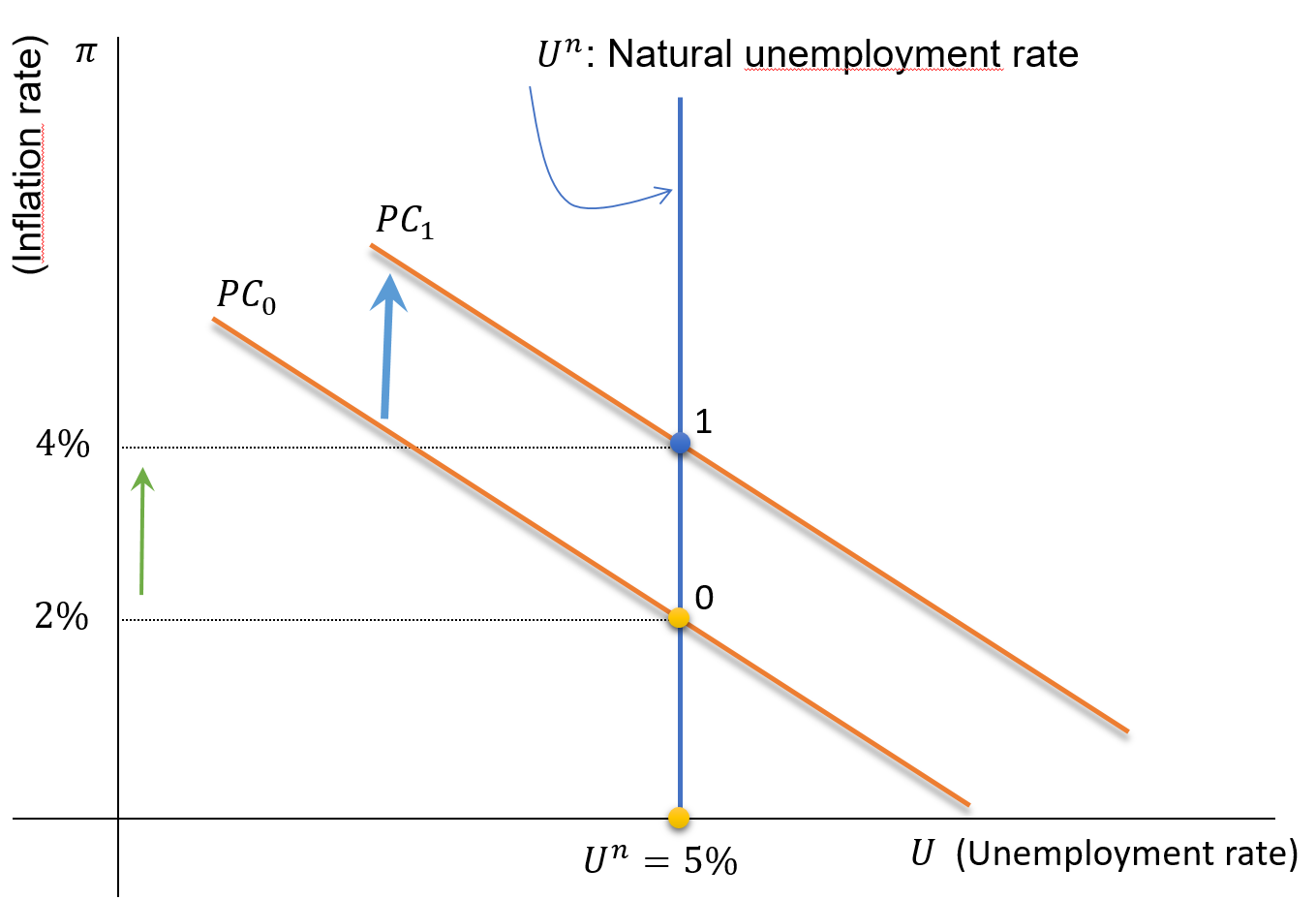
Shifts in the Phillips Curve \((\pi^e , \ \rho)\)

The PC shifts to the right if:
- \(\uparrow \pi^e\), \(~~\) or
- \(\uparrow \rho\)
Shifts in the Phillips Curve (\(U^n\))
\[\pi=\pi^e-\omega\left(U-U^n\right)+\rho \quad , \quad \color{black}{\pi^e=\pi_{-1}}\]
- The Phillips Curve shifts when the following forces change:
- Expected inflation (\(\pi^e\))
- Supply shocks (\(\rho\))
- Natural unemployment rate (\(U^n\))
- Let us concentrate on the last force (click on any key).
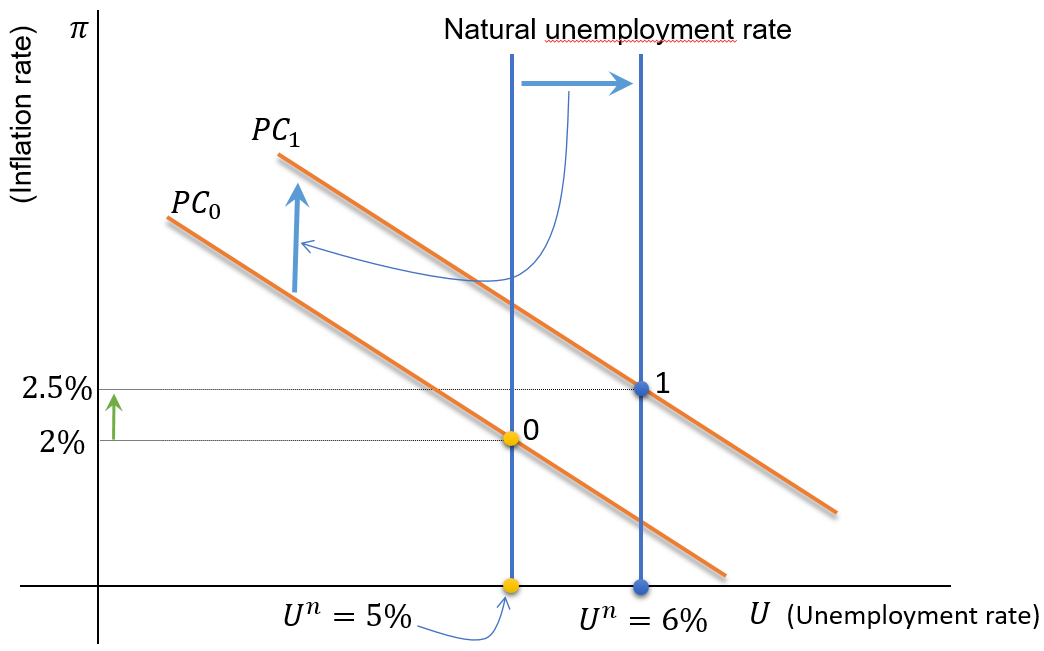
Shifts in the Phillips Curve (\(U^n\))

The PC will shift to the right if:
- \(\uparrow U^n\)
- Stable inflation will now be at 2.5%
Shifts in the PC: Inflationary Spiral Numerically
\[\pi=\pi^e-\omega\left(U-U^n\right)+\rho \quad , \quad \color{black}{\pi^e=\pi_{-1}}\]
- What happens if the government or the central bank try to keep the unemployment rate below the natural rate ?
- \(U<U^n\)
- The Phillips Curve will shift to the right
- \(U<U^n\)
- Inflationary expectations : inflation will increase systematically over time
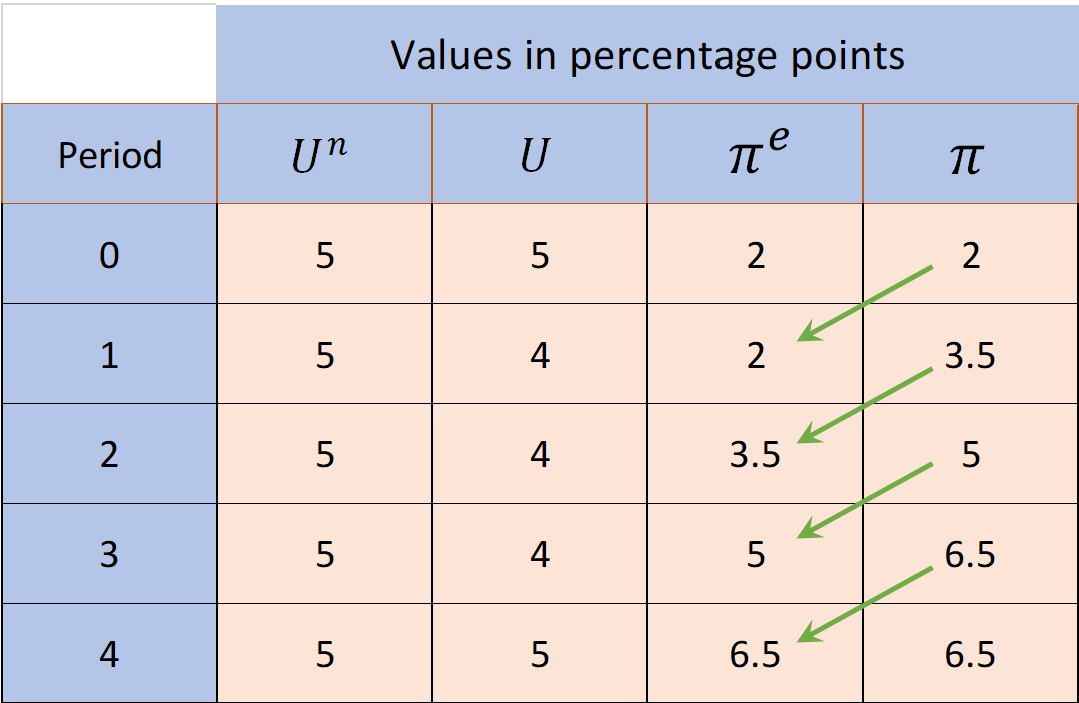
Shifts in the PC: Inflationary Spiral Numerically
\[\pi=\pi^e-\omega\left(U-U^n\right), \quad \omega=1.5, \quad \pi_t^e=\pi_{t-1}\]

- Suppose \(\pi _0 =2\%\)
- If, \(U_1<U^n_1\) Inflation will only stop if \(U\) returns to the \(U^n\) level
- But the result will be a higher \(\pi\) and the same initial \(U\)
Shifts in the PC: Inflationary Spiral Graphically
\[\pi=\pi^e-\omega\left(U-U^n\right), \quad \omega=1.5, \quad \pi_t^e=\pi_{t-1}\]
- The previous numerical example can be represented graphically
- Click on any key to continue
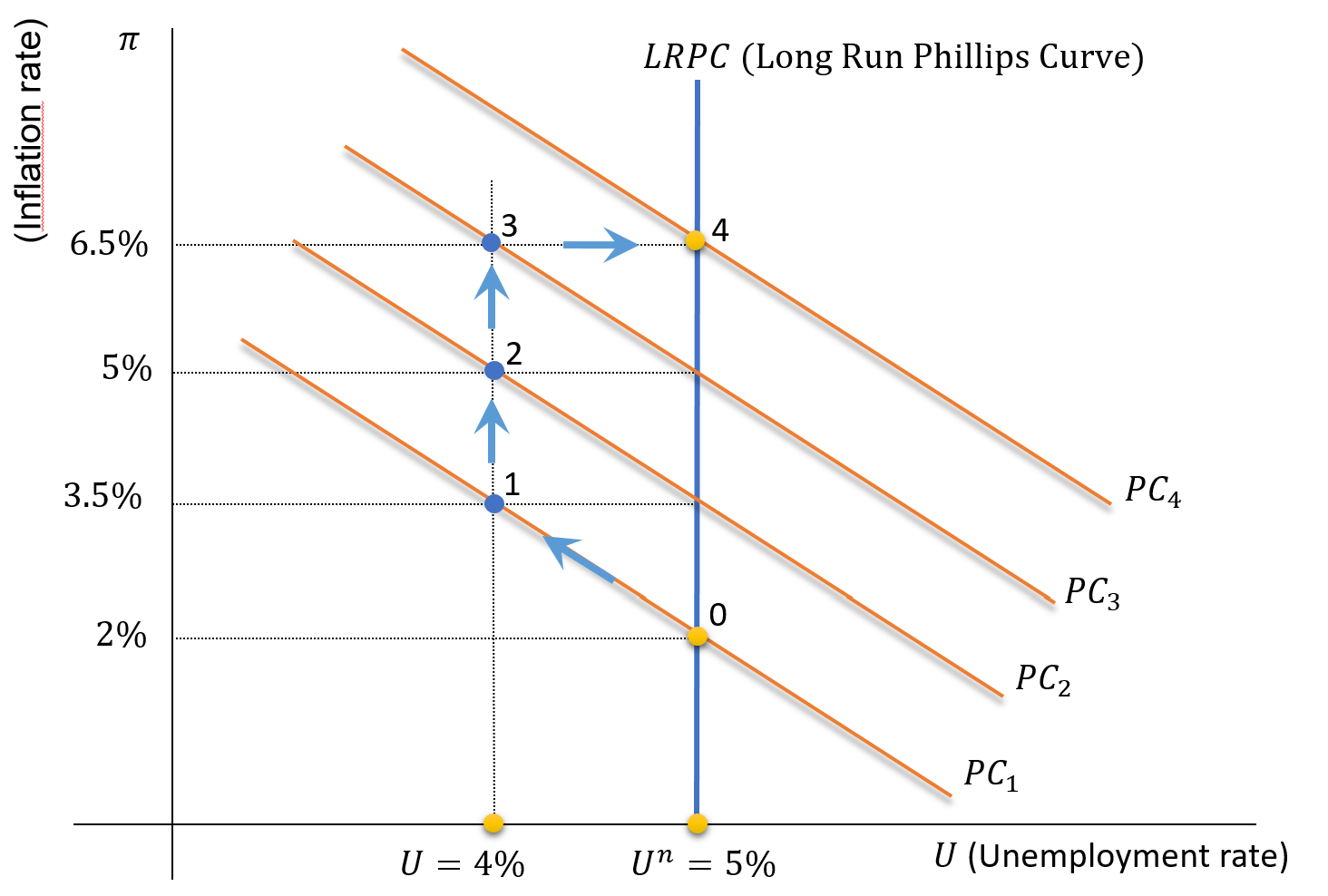
Shifts in the PC: Inflationary Spiral Graphically
\[\pi=\pi^e-\omega\left(U-U^n\right), \quad \omega=1.5, \quad \pi_t^e=\pi_{t-1}\]

- Suppose \(\pi _0 =2\%\)
- Inflation will only stop if the \(U\) returns to the \(U^n\) level
- But the result will be a higher \(\pi\) and the same initial \(U\)
3. The Okun’s Law
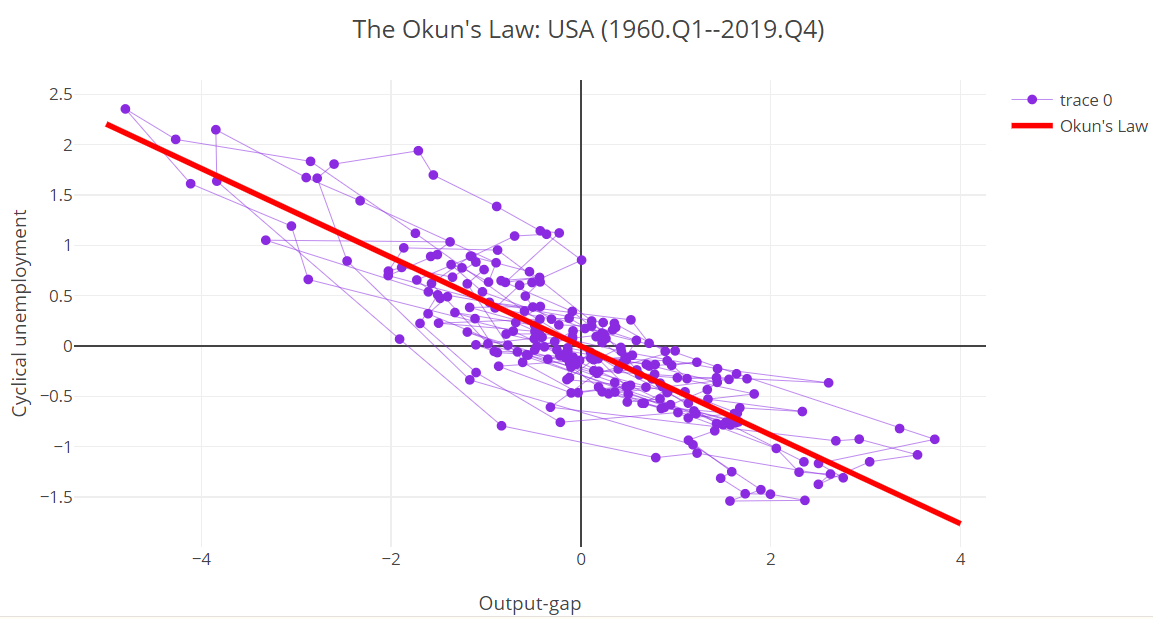
The Okun’s Law
Arthur Okun showed in the early 1960s that there is a negative relationship between cyclical unemployment and the output-gap: \[ \underbrace{U-U^n}_{\text {Cyclical unemployment }}=-\theta \times \underbrace{\left(Y-Y^P\right)}_{\text {Output-gap }} \]
where \(\theta\) is a parameter, for the USA economy usually close to: \[ \theta \simeq 0.5 \]
Arthur M. Okun (1962). “Potential GNP: Its Measurement and Significance”. Reprinted as Cowles Foundation Paper 190.
The Okun’s Law for the USA
The slope of the curve was \(−0.441\) for the period 1960-2019.
. . .
4. The Aggregate Supply Curve (AS)
The Short-Run AS Curve: Derivation
The Phillips Curve (PC): \[ \pi=\pi^e-\omega\left(U-U^n\right)+\rho \]
The Okun’s law: \[ U-U^n=-\theta \times\left(Y-Y^P\right) \]
The short-run Aggregate Supply curve (AS) is obtained by inserting the Okun’s law into the Phillips Curve (PC). Therefore: \[ \pi=\pi^e-\omega \times \underbrace{\left[-\theta\left(Y-Y^P\right)\right]}_{=U-U^n}+\rho \tag{7.5} \]
To simplify notation we will use: \(\gamma=\omega \theta\).
So, the short-run AS curve is given by: \[ \pi=\pi^e+\gamma\left(Y-Y^P\right)+\rho \tag{7.6} \]
The AS Curve: Graphical Representation
\[ \pi=\pi^e+\gamma\left(Y-Y^P\right)+\rho \quad , \quad \pi^e = \pi_{-1} \]
. . .
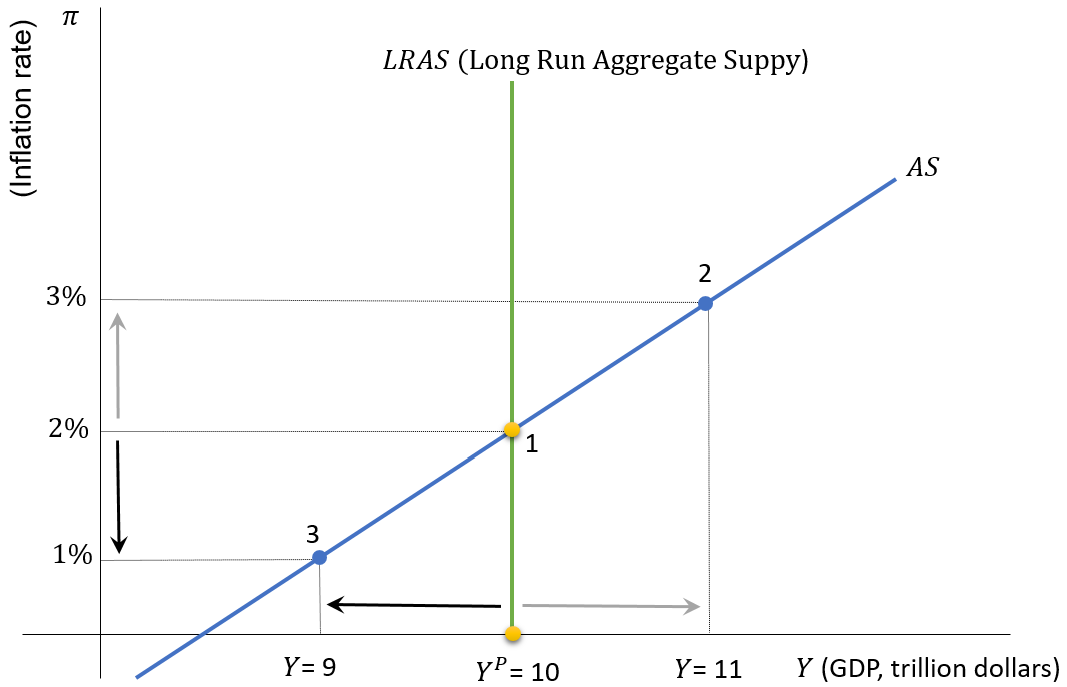
- In 1, \(Y=Y^P\)
- In 2, \(Y>Y^P\), economic boom, \(\pi\) increases to \(3\%\)
- In 3, \(Y<Y^P\), economic recession, \(\pi\) decreases to \(1\%\)
Shifts in the AS Curve (\(\pi^e, \rho\))
\[ \pi=\pi^e+\gamma\left(Y-Y^P\right)+\rho \quad , \quad \pi^e = \pi_{-1} \]
- The AS Curve shifts when the following forces change:
- Expected inflation (\(\pi^e\))
- Supply shocks (\(\rho\))
- Potential GDP (\(Y^P\))
- Let us concentrate on the two first forces (click on any key).
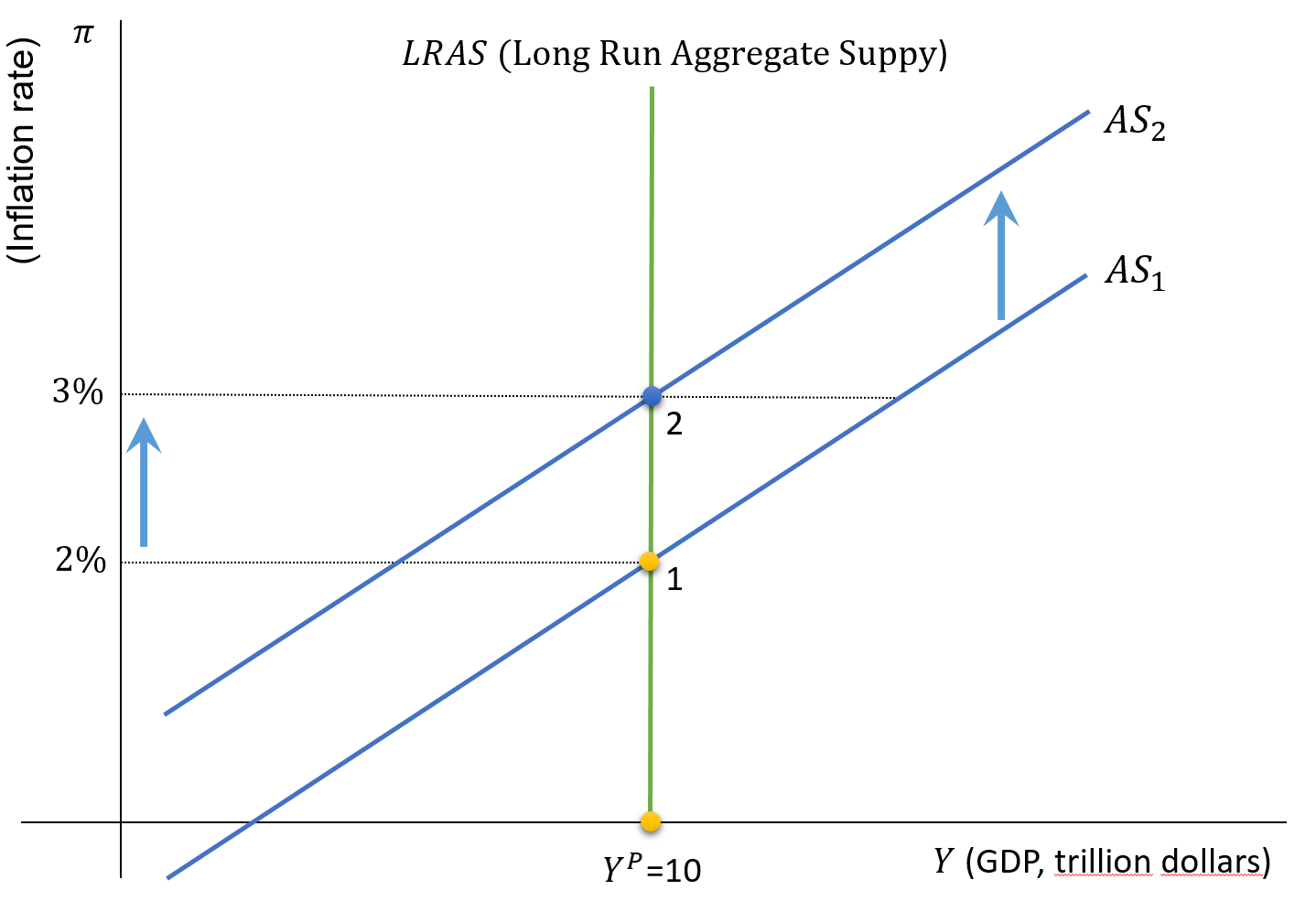
Shifts in the AS Curve (\(\pi^e, \rho\))

The AS shifts to the left if:
- \(\uparrow \pi^e\), or
- \(\uparrow \rho\)
Shifts in the AS Curve (\(Y^P\))
\[ \pi=\pi^e+\gamma\left(Y-Y^P\right)+\rho \quad , \quad \pi^e = \pi_{-1} \]
- The AS Curve shifts when the following forces change:
- Expected inflation (\(\pi^e\))
- Supply shocks (\(\rho\))]
- Potential GDP (\(Y^P\))
- Let us concentrate on the last force (click on any key).
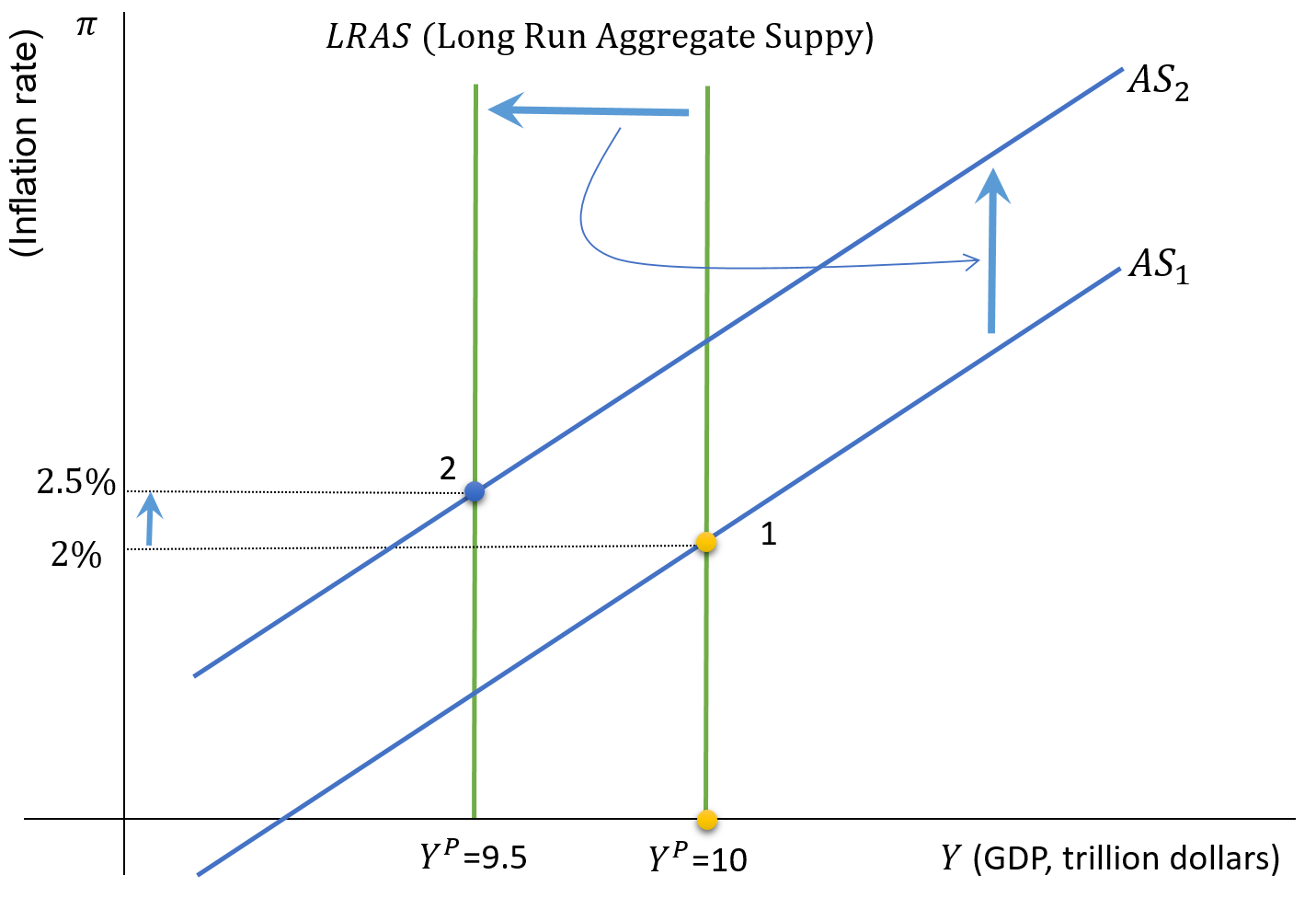
Shifts in the AS Curve (\(Y^P\))

AS shifts to the left if:
- \(\downarrow Y^P\)
- The economy will have stable \(\pi\) only at point 2.
- At 2: \(\ \downarrow Y \ \) , \(\ \uparrow \pi\)
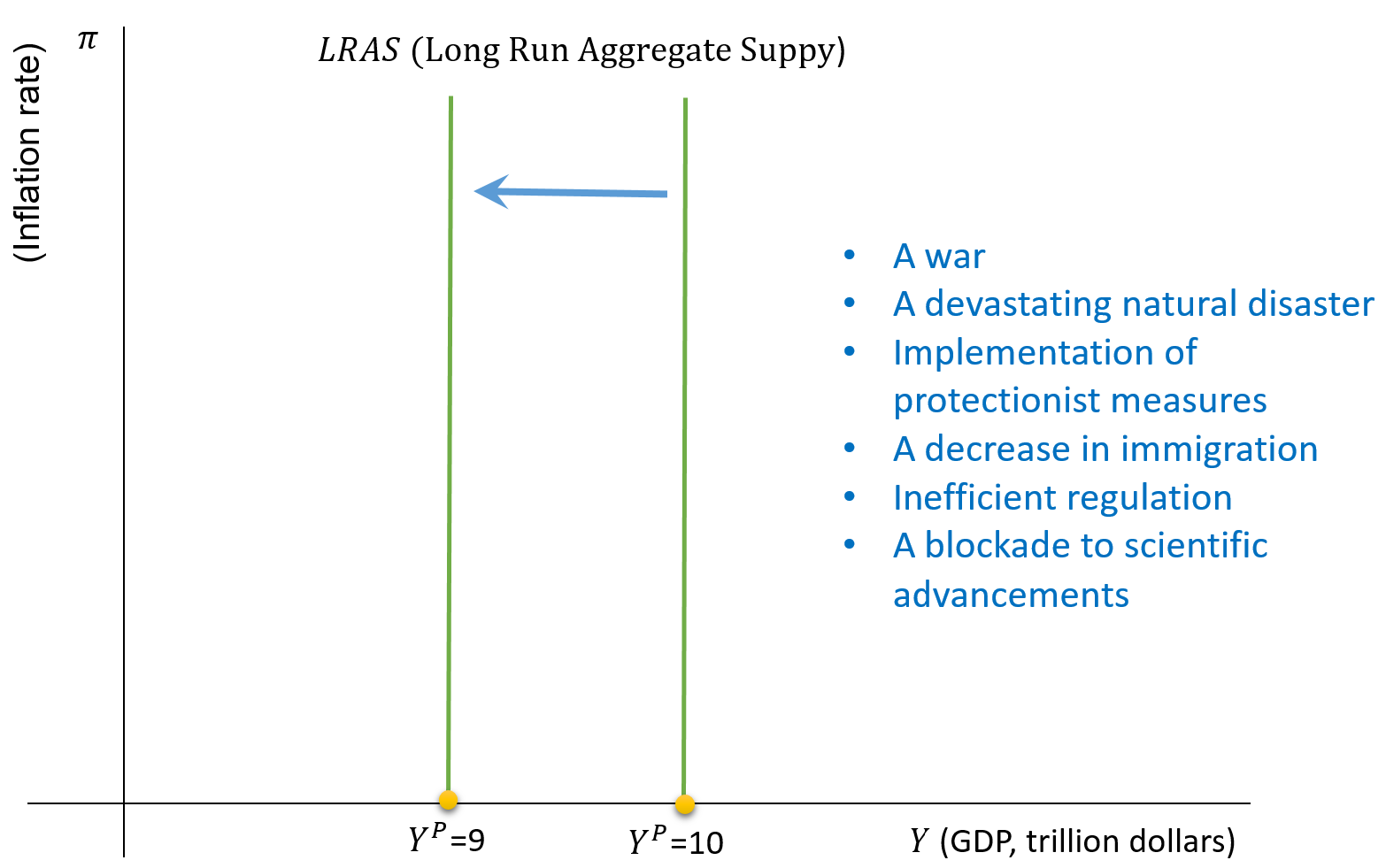
What Factors Shift the LRAS Curve?
- The factors that shift the LRAS curve are those that shift the production function studied in your Microeconomics course.
- The production function is given by: \[ Y=F(\cal{T}, K, L) \]
- The factors that shift the production function are:
- \(\cal{T}\): Technology
- \(\cal{ K}\): Capital
- \(\cal{L}\): Labor
What Factors Shift the LRAS Curve?
Forces reducing any of the factors \(\{\cal{T}, K, L\}\) shift the LRAS to the left, and vice-versa.
5. Readings
Readings
Read Chapter 11 of the adopted textbook:
Frederic S. Mishkin (2015). Macroeconomics: Policy & Practice, Second Edition, Pearson Editors.